Exercice n°2 BTS Biochimiste 2003

beer1

Corrigé

1.   Transmittance : T = Φt / Φi C’est le rapport du flux transmis au flux incident.

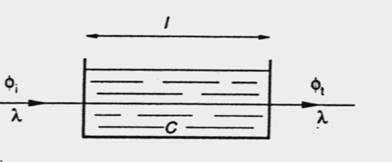
 msoCE379

Absorbance : A = log (1/T).

 

2.  Loi de Beer-Lambert : A = e.l.c

A est l’absorbance de la solution, e est le coefficient d’absorbance linéique molaire (m².mol-1), l est la longueur de la cuve (en m) et c la concentration de la solution (en mol.m-3).

3.   On choisit la longueur d’onde qui correspond à l’absorption maximale pour la solution considérée. En effet, comme la lumière employée n’est pas parfaitement monochromatique, on travaille au maximum d’absorption pour que e puisse être considéré comme constant (Au niveau du pic d’absorption, e est quasiment identique pour le domaine très restreint de longueurs d’ondes employées.)

On travaille également à cette longueur d’onde pour avoir des valeurs d’absorbances élevées afin de minimiser les erreurs relatives de mesures.

4.  Relation entre la concentration massique et la concentration molaire : c =  et 1 mol.L-1  = 103 mol.m-3

On peut donc compléter le tableau :

r (g.L-1)

0.60 10-3

1.50 10-3

2.40 10-3

3.00 10-3

4.50 10-3

6.00 10-3

A

0.075

0.250

0.420

0.515

0.775

1.040

c (mol.L-1)

1.47 10-6

3.67 10-6

5.88 10-6

7.35 10-6

1.10 10-5

1.47 10-5

c (mol.m-3)

1.47.10-3

3.67 10-3

5.88 10-3

7.35 10-3

1.10 10-2

1.47 10-2

On trace A = f(c) puisque e et l sont des constantes, on devrait obtenir une droite qui passe par 0.

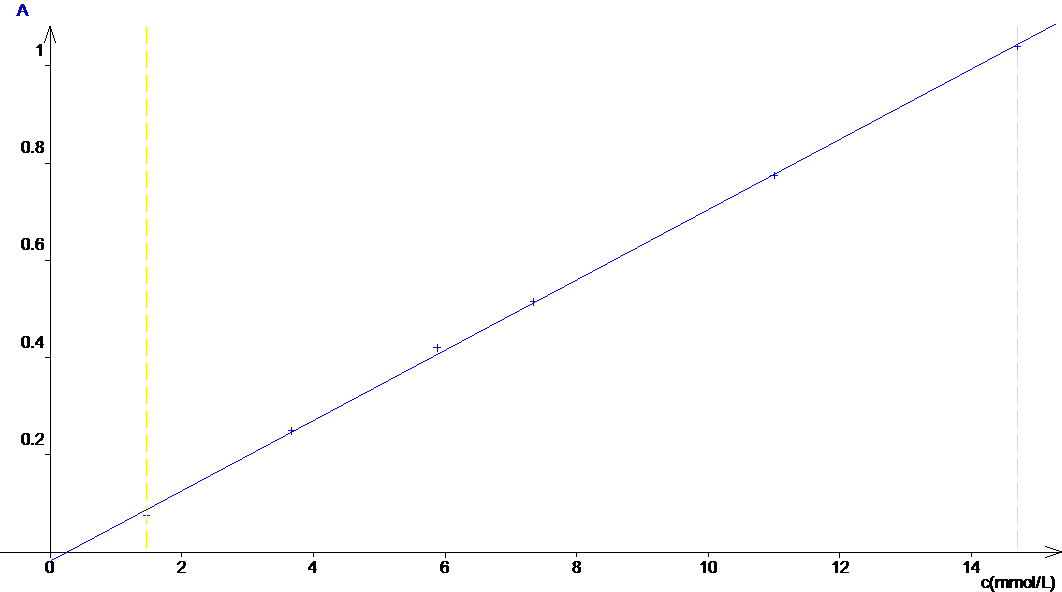
On obtient une droite qui passe par 0 : la loi de Beer-Lambert est vérifiée.

L’équation de la droite est A = 72.3.c

Remarque : La valeur de b obtenue ( b=0.02) est suffisamment proche de 0 pour qu’on admette que la droite passe par 0.

 

On peut également effectuer une régression linéaire à la calculatrice.

La régression linéaire donne un coefficient de corrélation r=0.999, on est bien en présence d’une droite puisque r>0.99. L’équation de la droite donnée par la calculatrice est A = 72.4.c. la valeur de « b » ( de y = ax+b) est suffisamment faible pour être assimilable à 0.

 

5.   On a A = e.l.c et A = 72.3.c donc e.l = 72.3 soit e =  =  = 7.23 103 m².mol-1.

6.  On a A = e.l.c   donc c =  =  =  7.34 10-3 mol.m-3 soit 7.34 10-6 mol.L-1.

Puisque c =  on a r = c.M = 2.99 10-3 g.L-1.

Cette valeur est très proche de celle obtenue pour A = 0.515, mais inférieure, ce qui parait illogique. La limite de la précision des mesures ne permet pas de donner toutes les valeurs du tableau à 3 chiffres significatifs.