Exercice n°4

On étudie la saponification du méthanoate d’éthyle qui produit de l’éthanol et l’ion méthanoate.

1- A t =0, on dispose de 0,01 mol/L de soude et d’ester. On suit l’évolution de la réaction au cours du temps et on note les résultats suivants à 25°C:

t en s	0	180	240	300	360
[alcool] en mmol/L	0	2.6	3.17	3.66	4.11

a) Montrer que la réaction est d’ordre global 2.

b) En déduire dans l’hypothèse la plus simple, les ordres partiels par rapport à chacun des réactifs.

2-Calculer en précisant les unités, la constante de vitesse à 25°C, et le temps de demi-réaction.

Corrigé

1. Afin de montrer que cette réaction est d’ordre 2, on doit d’abord déterminer les concentrations des réactifs.

a- On a : Dans V = 1L

	CH₃COOC₂H₅	+ OH^-	= CH₃COO^-	+ C₂H₅OH
EI	0.01	0.01	0	0
E(t)	0.01 -x	0.01-x	x	x

On remarque qu’à tout instant on a C = [CH₃COOC₂H₅] = [OH^-]

Comme x est donné dans le tableau ci-dessus, on peut déterminer 0.01-x en fonction du temps.

On peut également calculer 1/C en fonction du temps.

t en s	0	180	240	300	360
[alcool] en mmol/L	0	2.6	3.17	3.66	4.11
[CH₃COOC₂H₅] en mol/L	0.01	0.0074	0.00683	0.00634	0.00589
1/C	100	135.1	146.4	157.7	169.8

Afin de montrer que la réaction est d’ordre 2 on trace 1/C = f(t).

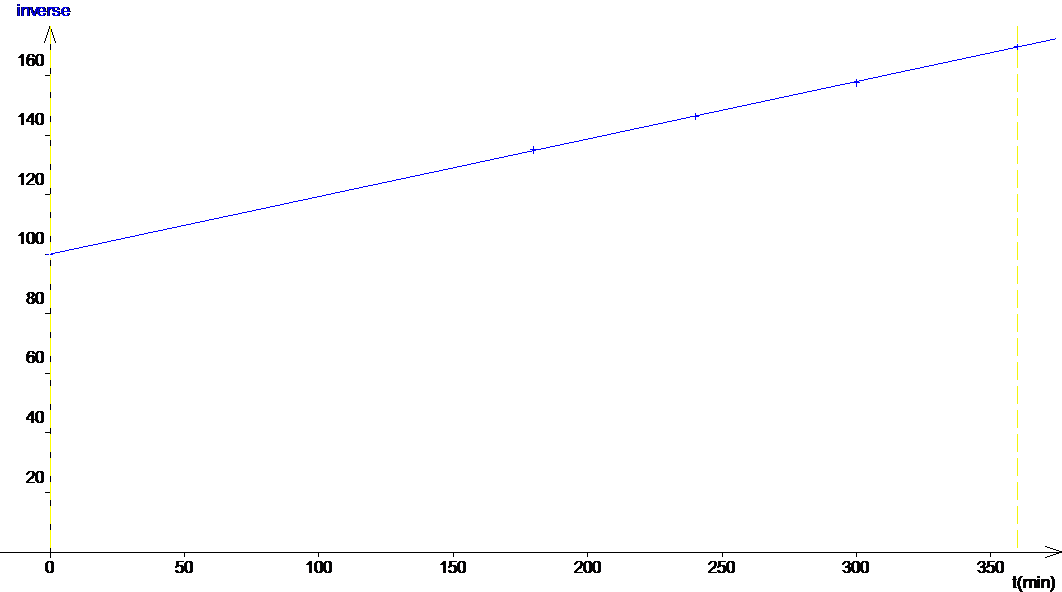
1/C en fonction du temps est une droite : la réaction est d’ordre 2.

L’équation de cette droite est 1/C = 0.193t + 100

b- l’hypothèse la plus probable est que les deux ordres partiels soient égaux à 1, et donc l’ordre global est égal à 2.

V = k [CH₃COOC₂H₅]¹[OH^-]¹

Or on a [CH₃COOC₂H₅] = [OH^-] à tout instant donc on peut écrire :

v = k [CH₃COOC₂H₅]² = k [OH^-]²

Il s’agit bien d’une réaction d’ordre global 2 et dont les ordres partiels sont égaux à 1.

2. La constante de vitesse correspond au coefficient directeur de la droite tracée ci-dessus.

On obtient k = 0.193 mol^-1.L.min^-1.

Pour déterminer T_1/2 à l’ordre 2 on emploie la formule T_1/2 = = = 518 minutes.

Ce résultat est cohérent avec les valeurs de C obtenues dans le tableau ci-dessus.