Exercice n°7

On dispose de deux flacons contenant de l’eau oxygénée de concentration 1 mol.L^-1 qui viennent juste d’être préparés. A l’instant t = 0, on introduit, sans variation de volume notable, une quantité de chlorure de fer III dans le flacon n°1. Le flacon n°2 est laissé tel quel.

Toutes les cinq minutes, on dose la quantité restante de H₂O₂ dans les deux flacons. La réaction qui a lieu dans les deux flacons est la décomposition de l’eau oxygénée :

2 H₂O₂ = O₂ + 2 H₂O.

On obtient les résultats suivants :

t (min)	0	5	10	15	20	25	30	35
Flacon n°1 [H2O2] mol.L^-1	1.0	0.81	0.66	0.53	0.43	0.35	0.28	0.23
Flacon n°2 [H2O2] mol.L^-1	1.0	Non effectué	Non effectué	Non effectué	Non effectué	Non effectué	Non effectué	0.99

Pour le flacon n°1 :

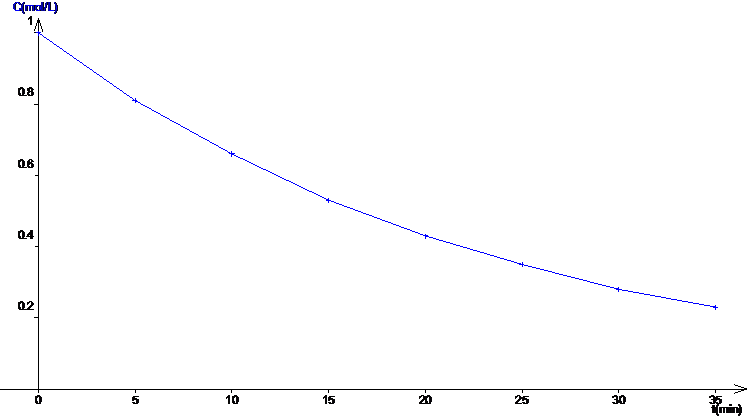
1. Représenter l’évolution de [H₂O₂] en fonction du temps, sur une feuille de papier millimétré. Echelle : 2 cm pour 5 minutes et 1cm pour 0.1 mol.L^-1. (Ce graphe sera représenté dans la partie supérieure de la feuille de papier millimétré (prise verticalement) de manière à laisser de la place à d’autres graphes en dessous.)

2. Calculer la vitesse de disparition moyenne de l’eau oxygénée entre les instants t = 5 minutes et t = 25 minutes.

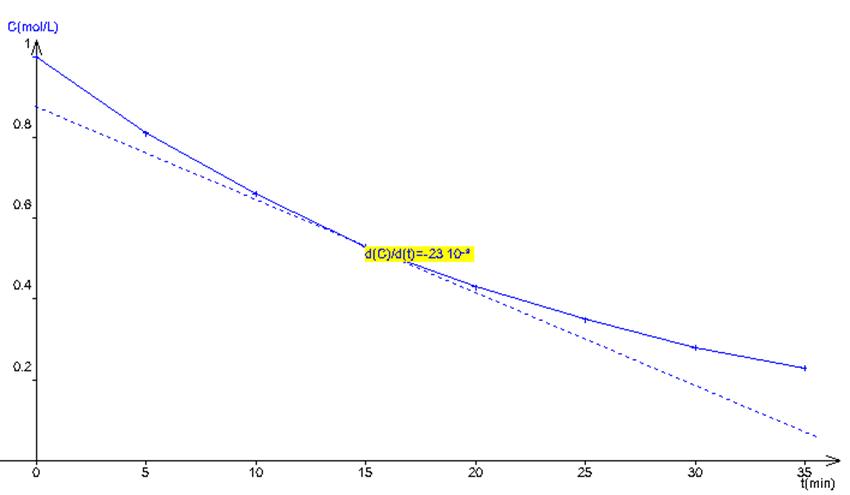
3. Déterminer la vitesse instantanée de disparition de l’eau oxygénée à t = 15 minutes.

4. En déduire la vitesse de réaction à cet instant.

5. Déterminer graphiquement l’ordre de cette réaction. (Il ne peut s’agir que d’une réaction d’ordres 0, 1 ou 2). Le ou les graphes seront réalisés sous le graphe de la question 1.1 avec des échelles convenables (éventuellement sous le graphe de physique, en cas de manque de place).

6. Déterminer la constante de vitesse de cette réaction chimique ainsi que le temps de demi-réaction par la méthode de votre choix.

7. Donner la relation exprimant la concentration restante d’eau oxygénée, C, en fonction de la concentration initiale, C₀, et du temps écoulé, t.

8. Que peut-on dire de l’évolution de la concentration de l’eau oxygénée dans le flacon n°2 ? Quel est le rôle d’un catalyseur ?

9. Sachant que le chlorure de fer est en solution dans le flacon n°1, parle t-on de catalyse homogène ou hétérogène ? Justifier votre réponse.

Corrigé

1	C = f(t) C = [H2O2]. t est exprimé en minutes.
2	Vm = - (C25 – C5) / 20 = - (0.35 – 0.81) / 20 = 0.023 mol.L^-1.min^-1.
3	Le coefficient directeur de la tangente à la courbe pour t = 15 minutes est a= - 0.023. On peut en conclure, qu’à cet instant, la vitesse de disparition instantanée de H2O2 est V15 = |a| = 0.023 mol.L^-1.min^-1.
4	Vréaction = VH2O2 = 0.011 mol.L^-1.min^-1 à t = 15 minutes. On a divisé par 2 car le coefficient stœchiométrique de H2O2 est 2.
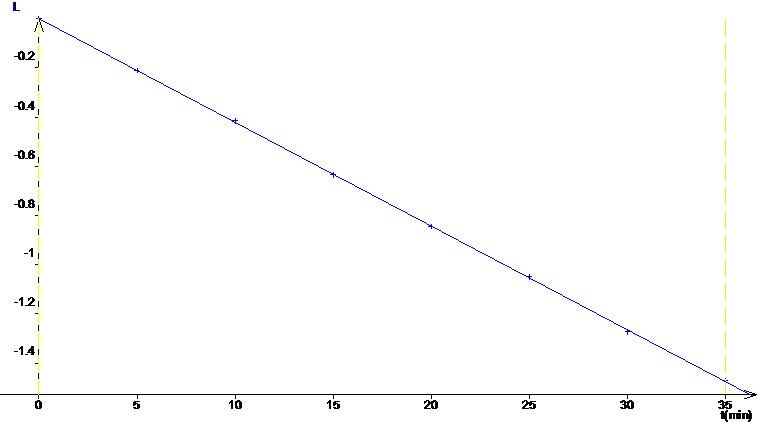
5	On trace Ln [H2O2] = f(t). Sur le graphique on a posé L = Ln [H2O2]. On obtient une droite de coefficient directeur a’ = -0.042 Il s’agit donc d’une réaction d’ordre 1. Remarque : La tracé de 1/C = f(t) ne donne pas une droite, ce qui exclue l’ordre 2, et C=f(t) n’étant pas une droite, l’ordre 0 est également exclu.
6	D’après la question précédente, on a k = |a |= 0.042 min^-1. Et τ = ln (2) / k = 16.5 minutes. Remarque : on peut déterminer τ graphiquement sur la courbe C = f(t) puis calculer k.
7	Puisqu’il s’agit d’une réaction d’ordre 1 : C = C0 e^-kt
8	On peut dire que la concentration d’eau oxygénée n’a pratiquement pas variée. Elle a diminué de façon minime. Le rôle d’un catalyseur est d’accélérer une réaction chimique.
9	On parle de catalyse homogène puisque le catalyseur est dans le même état physique que les réactifs.