Exercice n°8 type BTS.

On donne la réaction redox concernant les ions persulfates et iodures suivante :

S₂O₈^2- + 2 I^- = 2 SO₄^2- + I₂

Dans un premier temps, on introduit dans le mélange réactionnel, un très large excès d’ions iodures, de sorte que l’on puisse faire l’approximation que la concentration en ions iodures reste constante au cours du temps.

On a pour la première expérience les données suivantes :

Θ₁ = 25.5 °C ; [S₂O₈^2-]₀ = 0.010 mol.L^-1 et [ I^-]₀ = 1.0 mol.L^-1.

On mesure la concentration restante d’ions persulfate dans le mélange réactionnel à différents instants et on obtient le résultat suivant :

t(s)	[S2O8^2-] mol.L^-1
0	0,01
10	0,00943
20	0,00889
50	0,00745
75	0,00642
100	0,00554
150	0,00413
200	0,00307

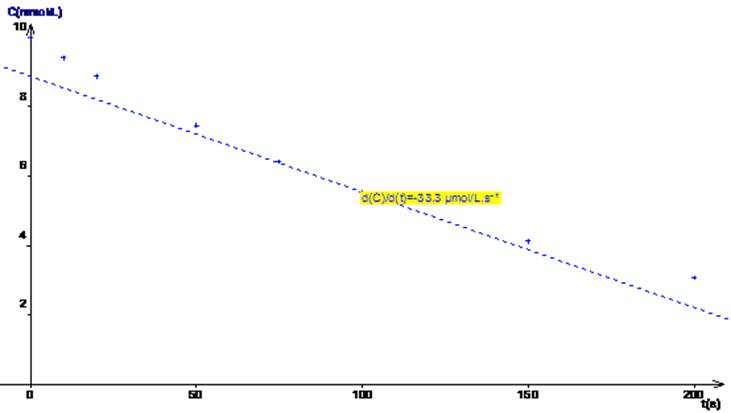
1. Déterminer la vitesse instantanée de disparition du persulfate à t = 100 s.

2. Déterminer, par la méthode de votre choix, l’ordre partiel de réaction par rapport au persulfate. Expliquez votre démarche.

On a déterminé par ailleurs que cette réaction était du premier ordre par rapport à l’ion iodure.

3. Proposer une méthode expérimentale ayant permis de déterminer cet ordre partiel de réaction.

4. Donner la relation indiquant la vitesse de réaction en fonction des concentrations en ions iodures et persulfate ainsi que de la constante de vitesse k₁. Quel est l’ordre global de cette réaction ?

5. Dans les conditions expérimentales indiquées ci-dessus, et en considérant que la concentration en ions iodures ne varie pas au cours de l’expérience, déterminer la constante de vitesse k₁.

6. Dans les mêmes conditions, établir la loi d’évolution de la concentration de persulfate au cours du temps : [S₂O₈^2-] = f (t).

7. Cette expérience a été réalisée à une température différente, et on a pu calculer une nouvelle constante de vitesse associée à cette température : θ₂ = 34°C, k₂ = 0.0108 USI. A l’aide de la loi d’Arrhenius, déterminer la valeur de l’énergie d’activation de cette réaction chimique.

Donnée : R = 8.31 J.mol^-1.K^-1_.

Corrigé

1	Le coefficient directeur de la tangente à la courbe c=f(t) à t = 100 s est a= -33.3 10^-6 mol.L^-1s^-1. C représente [S2O8^2-]. Donc la vitesse instantanée de disparition des ions persulfate est VD = 33.3 10^-6 mol.L^-1.s^-1.
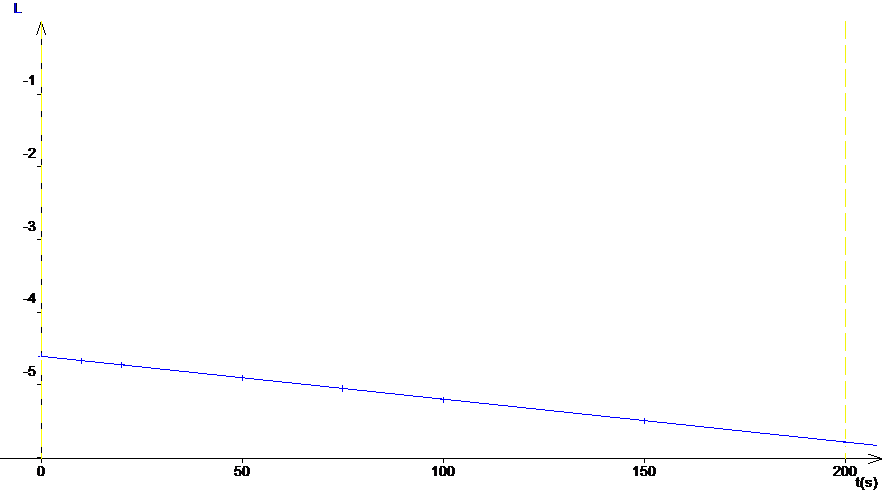
2	On peut procéder par régression linéaire à l’aide de la calculatrice ou tracer la courbe. On obtient une droite pour la courbe Ln (c) = f (t). L’équation de la droite est Ln(c) = -5.9.10^-3 t – 4.605. On obtient une droite pour le tracé de Ln(c) = f (t) (et seulement pour ce tracé, c=f(t) et 1/c = f(t) ne sont pas des droites) on peut donc en déduire que la réaction est d’ordre 1 par rapport à ce réactif.
3	On a pu procéder de la même manière que précédemment : On a mis un large excès de persulfate, de manière à ce qu’on puisse considérer que sa concentration reste constante au cours du temps. On peut déduire la quantité restante d’ions iodures à chaque instant en connaissant la quantité produite de I2 à chaque instant. Cette dernière peut être déterminée par photométrie, I2 étant une espèce colorée qui absorbe la lumière visible. Disposant de l’évolution de la concentration de l’ion iodure en fonction du temps, on peut vérifier que la réaction est d’ordre 1 par rapport à ce réactif en traçant Ln ([I^-]) = f(t).
4	VR = k1 [S2O8^2-]^1. [ I^-]^1 la réaction est globalement d’ordre 2 puisque l’ordre de réaction correspond à la somme des ordres partiels.
5	On a [ I^-] = [ I^-]0 = constante. Donc VR = k’ [S2O8^2-]. avec k’ = k1 [ I^-]0. k’ correspond à la constante de vitesse d’une réaction d’ordre 1 ne concernant que l’ion persulfate. k’ correspond donc à la valeur absolue du coefficient directeur de la droite Ln(C) = f(t). Soit k’ = 5.9 10^-3 s^-1. Et k1 = k’/[I]0 = 5.9 10^-3 L.mol^-1.s^-1. k1=k’ puisque [I]0 = 1 mol.L^-1.
6	Dans ces conditions, on peut traiter la réaction comme une réaction d’ordre 1 ne dépendant que d’un seul réactif : On a VR = k’ c et VR = - dc/dt. donc on a k^’ c = -dc/dt soit dc/c = -k^’ dt et ∫ dc/c = -k’ ∫ dt Donc [lnc] = -k’ [t] soit Lnc = - k’ t + « constante » Comme à t=0 c=c0 on en déduit que « constante » = Lnc0. lnc – lnc0 = -k’ t ou encore ln c/c0 = -k’ t. Soit c= c0 e^-k1t c0 étant la concentration initiale. Avec les valeurs numériques : c = 0.010 e^- 0.0059t.
7	Loi d’Arrhenius : k = A e^- Ea/RT et T = θ + 273.15 soit T1 =299 K et T2 = 307 K. Donc Ln k = LnA – Ea/RT Et Ln k1 – Ln k2 = Ea/RT1 + Ea /RT2 = Ea (-1/RT1 + 1/RT2) Soit Ea = (Ln k1 – Ln k2)/ (1/RT1 + 1/RT2) = 58 kJ.mol^-1.