Exercice n°3
Donnée : µ0= 4π 10-7
S.I
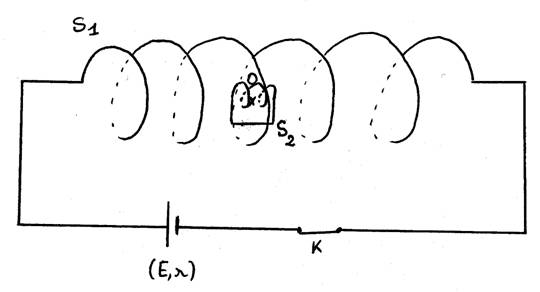
Un solénoïde S1 de 80cm de long est formé de 1000 spires ; il a
une résistance R=2.0 Ω. On le branche aux bornes d’une pile de force
électromotrice E=4,5V et de résistance interne r=3.0 Ω.
1.
Représenter, en
justifiant, le vecteur 
au point O (schéma
ci-dessus).
2.
Calculer l’intensité
du champ magnétique à l’intérieur du solénoïde S1.
Dans la suite, on prendra B=3,8.10-4T.
Dans le solénoïde S1
est placée une petite bobine S2 de 2.0 cm
de diamètre formée de 10 spires.
3.
Calculer le flux du
champ magnétique à travers la bobine.
4.
On ouvre
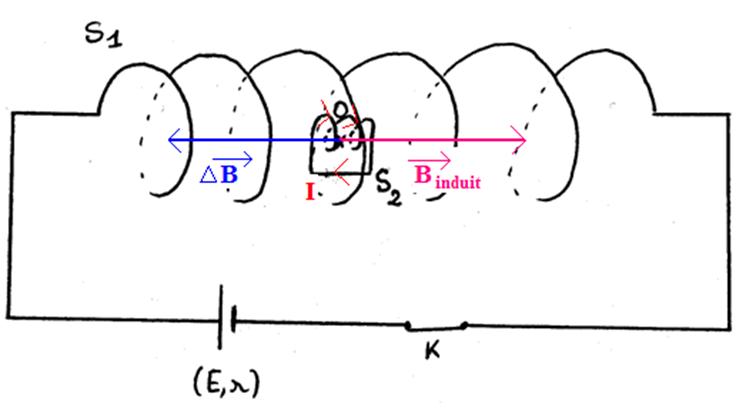
l’interrupteur K. Précisez le sens du courant induit créé dans cette bobine.
Corrigé
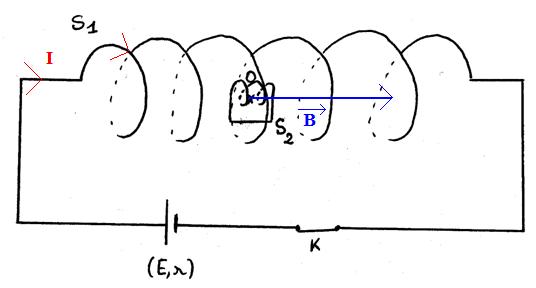
1. On
a appliqué la règle du tire-bouchon pour déterminer le sens de
.
2. On
détermine d’abord l’intensité du courant électrique, I, qui circule dans ce
circuit série. On peut appliquer la loi de Pouillet : I = 
= 0.90 A.
On a B1 = 
= 1.4 10-3 T.
3. Soit S la surface de la bobine S2 : S = p.R² = p.(2.10-2)² = 1.3 10-3 m².
Le flux qui traverse cette bobine
est f1
= NB1S cos a
avec a
qui est l’angle entre et 
.
étant parallèle à l’axe de la bobine S2,
il est colinéaire à et a =0. f1 = 1.8 10-5
Wb.
4. Lorsqu’on
ouvre le circuit, le champ magnétique s’annule donc 
= 
On peut en déduire 
= -
Soit = - = - .
D’après la loi de Lenz, on sait que 
s’oppose à et que le courant qui a donné naissance à suit la règle du tire-bouchon.
On en déduit le sens de I dans la bobine S2 sur le schéma suivant :
