Exercice n°3

Un noyau de radium ₈₈²²⁶Ra se désintègre spontanément en émettant un noyau d’hélium ₂⁴He.

1. De quel type de radioactivité s’agit-il ?

2. Que représentent les nombres 88 et 226 pour le noyau de radium ?

3. Ecrire l’équation de désintégration, en précisant les lois de conservation utilisées. Identifier le nouveau nucléide formé. (utiliser le tableau périodique)

4. Le nucléide X formé est lui aussi radioactif. Sa période radioactive est T = 3.8 jours. On considère une masse m₀ = 1mg de ce nucléide à une date choisie comme origine des temps.

a- Que représente T ?

b- Quelle masse de ce nucléide reste-t-il aux instants T, 2T, 3T, nT ?

c- Donner l’allure de la courbe de décroissance.

d- A quelle date la masse de nucléide restant sera-t-elle égale à m=0.0325 mg ?

Corrigé

1. Il s’agit d’une radioactivité α.

2. 88 est le nombre de charges du radium, il correspond à son nombre de protons. 226 est son nombre de masse il correspond à son nombre total de nucléons dans le noyau.

3. ₈₈ ²²⁶Ra → ₈₆²²²Rn + ₂⁴He + γ.

4. a- T représente la période radioactive de ce radioélément.

b- Au bout d’une période la masse est divisée par deux :

m₁ = 0.5 mg.

Si t = 2T m₂ = m₀/2² = 0.25 mg.
Si t= 3T m₃ = m₀ / 2³ = 0.125 mg.

Si t= nT alors m_n = m₀ / 2ⁿ.

c- Courbe de décroissance radioactive :

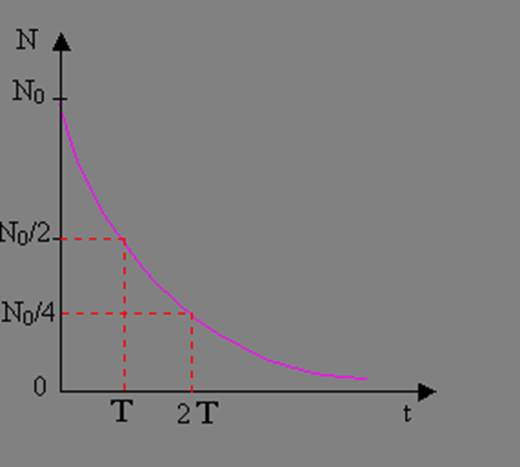
N : Nombre de noyaux à l’instant t.

N₀ : Nombre de noyaux initial.

t : Temps écoulé (s, min, h, j, ans).

T : période radioactive (s, min, h, j, ans).

d- On a m = m₀ e^-λt donc m/m₀ = e^-λt et ln (m/m₀) = -λt soit encore t = t =

λ = ln 2 /T =0.18 j^-1 et t t = = = 18.8 j.