Exercice n°6
Le noyau de bismuth 212 83Bi
se désintègre spontanément en noyau de thallium Tl avec émission d’une particule
α.
1. Ecrire l’équation de la désintégration en indiquant
les nombres de charge et de masse du noyau de thallium et de la particule
α. Préciser les lois utilisées.
2. Certains noyaux de thallium sont créés dans un état
excité. Voici un diagramme simplifié représentant les niveaux d’énergie du
thallium :
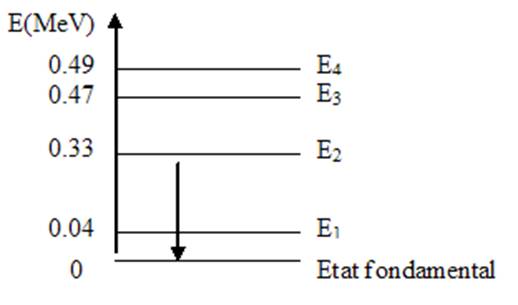
On
a représenté sur ce diagramme la transition énergétique correspondant à la
désexcitation d’un noyau de thallium. Calculer la longueur d’onde du photon
émis lors de cette transition énergétique. Dans quel domaine de rayonnement se
situe-t-il ?
3. La période du bismuth 212 est T=1h. A l’instant t=0,
un échantillon contient 1g de bismuth 212. Au bout de combien de temps n’en
restera-t-il plus que 0,125g ?
Données : h = 6.63 10-34 J.s ; C= 3.00
108 m.s-1 ; 1 Mev = 1.6 10-13 J.
Corrigé
1. 212 83Bi 
81208Tl
+ 24He + g
Le nombre de
charges du Thallium est 81 et son nombre de masse est 208.
On a
appliqué la loi de conservation du nombre de charges et la loi de conservation
du nombre de masse.
2. On a Eph
= E2 – E0 = 0.33 – 0 = 0.33 Mev = 0.33x1.6 10-13
= 5.28 10-14J
Or Eph
= 
et l = 
= 3.76 10-12
m = 3.76 10-3 nm Il s’agit d’un rayon X puisqu’il est compris entre
10-3 et 10 nm. Il est cependant à la limite des rayonnements g.
3. On remarque que 0.125 = 1/8 =1/23 On en
conclut donc que l amasse de l’échantillon s’est désintégrée de moitié à trois
reprises donc que 3 périodes ses sont écoulées soit 3 heures.
On peut
également résoudre cette question de manière classique :
On a N(t) =
N0 e-lt soit N/N0
= e-lt ou encore ln
(N/N0) = -lt
Soit t = 
Par ailleurs
on a l
= 0.693 h-1
Soit t = = 
= 3.0 heures.