Exercice n°1
Un échantillon de 10 mg d’iode ![]() est
radioactif b-. Il a une période T = 8 jours.
est
radioactif b-. Il a une période T = 8 jours.
1. Période, constante radioactive et loi de décroissance
1.1.Donner la définition de la période radioactive
T d’un élément ?
1.2.Calculer
la constante radioactive l
de l’iode 53131I.
1.3.Quelle masse d’iode 53131I reste-t-il
au bout de 24 jours ?
2. Désintégration de l’iode ![]()
Ecrire
l’équation-bilan de désintégration de l’iode 131. Indiquer les lois utilisées.
Calculer l’énergie libérée
par la désintégration d’un noyau d’iode ![]() en joule et en MeV.
en joule et en MeV.
3. Rayonnement émis lors
de la désintégration
La
désintégration d’un noyau 53131I s’accompagne d’une émission
g.
3.1
Quelle est la nature de ce rayonnement ?
3.2
Comment peut-on interpréter l’émission de ce rayonnement ?
Le diagramme énergétique
du noyau fils émis est le suivant :

• Extrait de la classification
périodique :
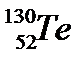 ;
; 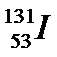 ;
; 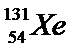
• Masses atomiques : M Te =
129,8782 u.m.a M I = 130,8770 u.m.a M Xe = 130,8754 u.m.a M électron
= 0,00055 u.m.a.
1u = 1.66 10-27 Kg = 931.5 MeV. c-2. 1 Mev = 1.6 10-13 J. h = 6.63 10-34 J.s
Corrigé
Exercice n°2
On donne la réaction suivante : 235U + 01n
® 60144Nd
+ Y + 3 01n + 7 –10e
1- sachant
qu’un noyau d’uranium 235 renferme 143 neutrons, compléter cette équation avec
les valeurs de nombres de charges et de masses manquantes.
2- De quel
type de réaction s’agit-il ?
3- Calculer, en Joule et en MeV, l’énergie libérée au cours de cette
réaction..
4- Quelle énergie
est libérée par la réaction complète de 500g d’Uranium 235 ?
5- Montrer
que le Néodyme (Nd) est plus stable que l’uranium.
Données : 1u = 1.66 10-27 Kg = 931.5 MeV. c-2. mU
= 235.12037 u ; mNd = 143.95060 u ; mY =
88.93712 u ;
mn
= 1.008665 u ; mp = 1.007276 u ; me = 5.5 10-4
u (masse de l’électron).
Corrigé
Exercice n°3
On dispose de l’isotope
radioactif 1124Na, c’est un radioélément β-
qui a une période radioactive d’environ 15 heures, dont la masse nucléaire est
de 23.991 u et la masse molaire voisine de 24 g.mol-1.
Au cours de sa
désintégration radioactive, il forme un noyau fils X de masse 23.985 u.
1.
donner la composition du
noyau de sodium 1124Na.
2.
Ecrire son équation de désintégration
et identifier le noyau X. (donner son nom, son numéro atomique et son nombre de
masse).
3.
déterminer l’énergie libérée
au cours de cette désintégration en Mev et en J.
4.
déterminer la constante
radioactive, λ, de cet élément.
5.
l’échantillon dont on
disposait avait une masse de 2.6 g. Au bout de combien de temps ne reste t’il
plus que 0.2 g de 1124Na.
6.
Calculer, en Joule,
l’énergie totale qui a été libérée pendant cette durée.
7.
Cet échantillon est conservé
dans un pilulier de plexiglas, lui même enfermé dans une armoire en aluminium.
Les laborantins travaillant dans cette pièce sont ils susceptibles de recevoir
des émissions dues à ce radioélément, ou sont-ils hors de tout danger ?
Justifier votre réponse.
Données :
h=6,63.10-34J.s. c =3.108m.s-1 ;1
MeV=1,6.10-13J. 1u =1,66.10-27kg ; 1 u = 931.5 Mev.
c-2 ; me = 5.5 10-4 u (masse de
l’électron).

Corrigé
Exercice n°4 (BTS Bioac 2006)
Depuis 1985, un projet de coopération internationale pour la
production d’énergie par fusion nucléaire est né. C’est le projet ITER
(International Thermonucléar Expérimental Réactor). L'objectif du projet ITER
est de démontrer la possibilité scientifique et technologique de la production
d'énergie par la fusion des atomes. Le site choisi pour la mise en œuvre de ITER
est le centre de recherche de Cadarache en France.
Parmi les réactions de fusion envisageables, on a la réaction
suivante :
13X + 12Y
→ abZ + 01n
1.
Déterminer les symboles chimiques X et Y, Z ainsi que a et b.
2.
Déterminer l’énergie libérée, en Mev et en Joules, par la fusion
d’un noyau X avec un noyau Y suivant la réaction ci-dessus.
On donne les masses des nucléides suivants : mX = 3.0155
u ; mY = 2.0136 u ;
mZ =4.0026 u ; mn =
1.0087 u.
3.
Quelle est l’énergie libérée par la production de 10g de l’élément
Z ? Comparer cette énergie avec celle libérée par la combustion d’une
tonne de pétrole (4.2 1010 J).
4.
Où ont lieu les réactions de fusion dans l’univers ?
5.
Le deutérium (12Y) peut être extrait de
l'eau. (Environ 0,015 % de l'hydrogène dans l'eau existe sous forme de
deutérium.) Le tritium (13X) doit être fabriqué, car il n'existe pas en
quantité suffisante dans la nature. Le tritium est radioactif bêta moins.
Ecrire l’équation de sa désintégration. Qu’est ce qu’une particule bêta
moins ?
6.
Sa période radioactive est de 12.3 ans. On a préparé 1.00 kg de
tritium en vue de réactions de fusion. L’échantillon reste inutilisé pendant
30.0 ans.
Quelle masse de ce nucléide reste t-il lorsque les 30.0 ans
sont écoulés ?
Evaluer le nombre de noyaux de tritium restant ainsi que
l’activité de l’échantillon lorsque les 30.0 ans sont écoulés.
Données : 1u =
1.66 10-27 kg ; 1u = 931.5 Mev.c-2 ; Mz
= 4.0 g.mol-1 ; MX = 3.0 g.Mol-1 ;
1eV = 1.6 10-19J ; NA = 6.02 1023.
Extrait du tableau périodique :
|
1 H |
|
|
|
2 He |
||||
|
3 Li |
4 Be |
5 B |
6 C |
7 N |
8 O |
9 F |
10 Ne |
|
Corrigé
Exercice n°5
On donne la réaction suivante : 90228Th
![]() 24He + Ra + g
24He + Ra + g
1. Compléter l’équation en indiquant les nombres de masse et de
charge manquants.
2. Quelles lois ont été employées au 1.
3. Calculer l’énergie libérée au cours de cette réaction en J et en
MeV.
4. Déterminer l’énergie de liaison du thorium.
Données :
mTh = 228.0287 u ; mHe = 4.0026 u ; mRa
= 224.0202 u ; mn = 1.008665 u ; mp = 1.007276
u.
Corrigé
Exercice n°6
On donne les masses de deux isotopes de l’uranium.
1. Calculer en Mev les énergies de liaisons par nucléons des noyaux 92235U
et 92238U.
2. Lequel de ces deux isotopes est le plus stable ?
Données :
m (92235U) = 234.9942 u ; m (92238U)
= 238.0508 u ; mn = 1.008665 u ; mp = 1.007276
u.
1
MeV=1,6.10-13J. 1u =1,66.10-27kg ; 1 u = 931.5 Mev.
c-2
Corrigé
Exercice n°7
Le noyau 4299Mo
(Molybdène) se désintègre en technétium 4399Tc.
1. a- Ecrire l’équation correspondant à cette
désintégration.
b-
Quelles lois a-t-on appliquées ?
2. Déterminer en MeV, l’énergie libérée au cours de cette
désintégration.
3. Environ 90% des noyaux de technétium formés sont dans
un état excité. Leur désexcitation mono-énergétique s’accompagne d’une émission
d’énergie 140 keV. Déterminer la longueur d’onde du rayonnement émis.
Données :
mMo = 98.88437 u ; mTc = 98.88235 u ; me
= 5.5 10-4u ; 1 eV = 1.6 10-19J ; h = 6.63 10-34J.s